To Which Family Does the Function Mc005-1.jpg Belong? Quadratic Square Root Exponential Reciprocal

Finding out the time complication of your code tin can help you lot develop better programs that run faster. Some functions are like shooting fish in a barrel to analyze, but when you take loops, and recursion might get a picayune trickier when you take recursion. After reading this post, you are able to derive the time complexity of any code.

In full general, you lot tin can determine the time complication by analyzing the program'south statements (go line past line). Withal, you take to be mindful how are the statements arranged. Suppose they are within a loop or have part calls or even recursion. All these factors affect the runtime of your code. Allow'southward see how to deal with these cases.

Large O Notation

How to calculate time complexity of any algorithm or program? The well-nigh common metric it'south using Big O notation.

Here are some highlights about Big O Notation:

• Big O notation is a framework to analyze and compare algorithms.
• Corporeality of work the CPU has to practise (time complexity) as the input size grows (towards infinity).
• Big O = Big Order part. Drop constants and lower social club terms. E.yard. O(iii*n^ii + 10n + ten) becomes O(n^2).
• Big O annotation cares almost the worst-instance scenario. E.g., when you want to sort and elements in the array are in contrary order for some sorting algorithms.

For instance, if you have a function that takes an array as an input, if you increase the number of elements in the drove, you all the same perform the aforementioned operations; you accept a constant runtime. On the other mitt, if the CPU'southward work grows proportionally to the input assortment size, y'all have a linear runtime O(n).

If we plot the nigh common Large O notation examples, we would take graph similar this:

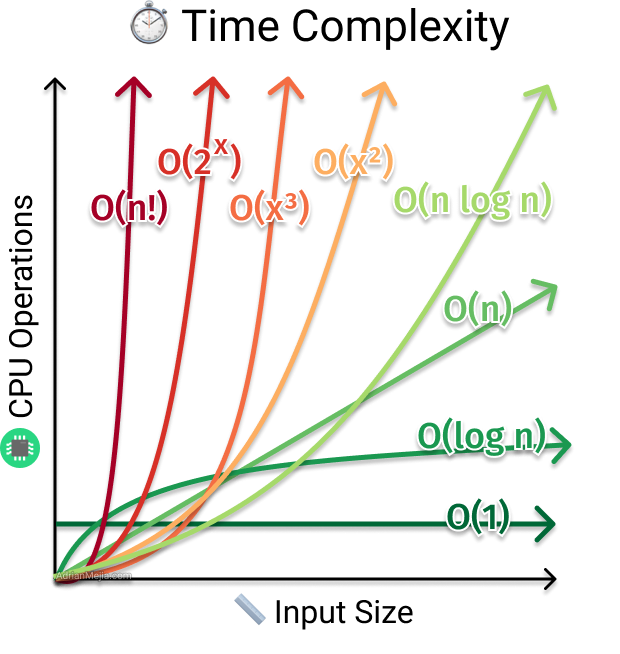
As yous tin see, you lot want to lower the time complexity function to accept better performance.

Permit's have a wait, how practice nosotros interpret code into time complexity.

Sequential Statements

If nosotros have statements with basic operations similar comparisons, assignments, reading a variable. We can assume they accept constant time each O(1).

1 2 3 4

statement1; statement2; ... statementN;

If we calculate the total time complexity, it would be something like this:

1	full = time(statement1) + time(statement2) + ... time (statementN)

Allow's use T(northward) as the total time in function of the input size n, and t as the time complication taken by a argument or grouping of statements.

ane	T(n) = t(statement1) + t(statement2) + ... + t(statementN);

If each argument executes a basic operation, nosotros can say information technology takes constant time O(1). As long as you have a stock-still number of operations, it will exist constant time, even if we have ane or 100 of these statements.

Example:

Let's say we can compute the foursquare sum of 3 numbers.

1 two 3 4 5 6 7

role squareSum(a, b, c) { const sa = a * a; const sb = b * b; const sc = c * c; const sum = sa + sb + sc; return sum; }

As you lot can see, each statement is a basic operation (math and assignment). Each line takes constant time O(1). If we add up all statements' fourth dimension it volition still be O(1). It doesn't matter if the numbers are 0 or 9,007,199,254,740,991, information technology will perform the same number of operations.

⚠️ Be conscientious with role calls. You will have to go to the implementation and check their run time. More on that later.

Conditional Statements

Very rarely, you have a lawmaking without any conditional statement. How do y'all summate the fourth dimension complexity? Remember that nosotros care about the worst-example with Big O so that we will take the maximum possible runtime.

1 2 3 four 5 half-dozen

if (isValid) { statement1; statement2; } else { statement3; }

Since we are later the worst-case we take whichever is larger:

1	T(northward) = Math.max([t(statement1) + t(statement2)], [time(statement3)])

Example:

ane two 3 4 five half-dozen

if (isValid) { array.sort(); return true; } else { return fake; }

What'south the runtime? The if block has a runtime of O(n log north) (that'southward mutual runtime for efficient sorting algorithms). The else cake has a runtime of O(1).

And so we have the following:

1	O([northward log n] + [due north]) => O(northward log n)

Since n log n has a college order than n, we can express the time complication as O(northward log due north).

Loop Statements

Another prevalent scenario is loops like for-loops or while-loops.

Linear Time Loops

For any loop, we find out the runtime of the block inside them and multiply it by the number of times the program will echo the loop.

ane 2 three 4

for (let i = 0; i < array.length; i++) { statement1; statement2; }

For this case, the loop is executed array.length, assuming n is the length of the array, nosotros get the following:

ane	T(n) = n * [ t(statement1) + t(statement2) ]

All loops that grow proportionally to the input size have a linear time complexity O(n). If y'all loop through only half of the array, that's yet O(due north). Remember that we drop the constants so one/2 n => O(n).

Abiding-Time Loops

However, if a constant number bounds the loop, let'southward say 4 (or fifty-fifty 400). Then, the runtime is constant O(four) -> O(1). Come across the following example.

one 2 3 4

for (let i = 0; i < 4; i++) { statement1; statement2; }

That code is O(1) considering it no longer depends on the input size. It will always run argument 1 and 2 four times.

Logarithmic Fourth dimension Loops

Consider the post-obit lawmaking, where we divide an array in half on each iteration (binary search):

1 2 3 iv five half-dozen 7 viii 9 10 xi 12

function fn1(array, target, low = 0, high = array.length - 1 ) { let mid; while ( low <= high ) { mid = ( depression + loftier ) / two; if ( target < array[mid] ) high = mid - 1; else if ( target > array[mid] ) low = mid + 1; else break; } return mid; }

This function divides the array by its middle signal on each iteration. The while loop will execute the amount of times that nosotros can divide array.length in half. Nosotros can calculate this using the log office. E.g. If the array's length is 8, so we the while loop volition execute three times considering log2(viii) = three.

Nested loops statements

Sometimes you might need to visit all the elements on a second array (grid/tabular array). For such cases, you might discover yourself with two nested loops.

1 two iii iv 5 6 7 8

for (let i = 0; i < n; i++) { statement1; for (let j = 0; j < k; j++) { statement2; statement3; } }

For this case, you lot would have something like this:

i	T(northward) = due north * [t(statement1) + m * t(statement2...three)]

Bold the statements from ane to 3 are O(one), we would take a runtime of O(north * grand). If instead of one thousand, you had to iterate on n again, then it would be O(n^ii). Another typical case is having a function inside a loop. Permit's run into how to deal with that next.

Role call statements

When you lot calculate your programs' time complexity and invoke a function, you lot need to exist enlightened of its runtime. If y'all created the part, that might exist a simple inspection of the implementation. If y'all are using a library function, you might need to check out the language/library documentation or source code.

Allow'southward say you have the post-obit program:

i 2 three 4 5 6 7 8 9

for (let i = 0; i < n; i++) { fn1(); for (let j = 0; j < n; j++) { fn2(); for (let thou = 0; k < n; k++) { fn3(); } } }

Depending on the runtime of fn1, fn2, and fn3, you would have different runtimes.

• If they all are constant O(i), then the concluding runtime would be O(n^3).
• All the same, if simply fn1 and fn2 are constant and fn3 has a runtime of O(n^2), this program will have a runtime of O(n^5). Another way to look at it is, if fn3 has two nested and you replace the invocation with the actual implementation, y'all would have 5 nested loops.

In general, you will have something like this:

1	T(northward) = n * [ t(fn1()) + northward * [ t(fn2()) + n * [ t(fn3()) ] ] ]

Recursive Functions Statements

Analyzing the runtime of recursive functions might get a picayune tricky. In that location are unlike means to do it. Ane intuitive mode is to explore the recursion tree.

Let'due south say that nosotros have the following programme:

1 2 3 4 5 6

function fn(n) { if (due north < 0) render 0; if (n < 2) render n; render fn(n - ane) + fn(due north - 2); }

You can correspond each function invocation as a bubble (or node).

Let'south do some examples:

• When you due north = 2, you have 3 function calls. First fn(2) which in turn calls fn(1) and fn(0).
• For northward = 3, y'all have 5 part calls. First fn(three), which in plough calls fn(ii) and fn(one) and and then on.
• For n = 4, you take 9 function calls. First fn(4), which in turn calls fn(3) and fn(2) and so on.

Since information technology's a binary tree, we can sense that every time n increases by one, nosotros would take to perform at virtually the double of operations.

Here's the graphical representation of the 3 examples:

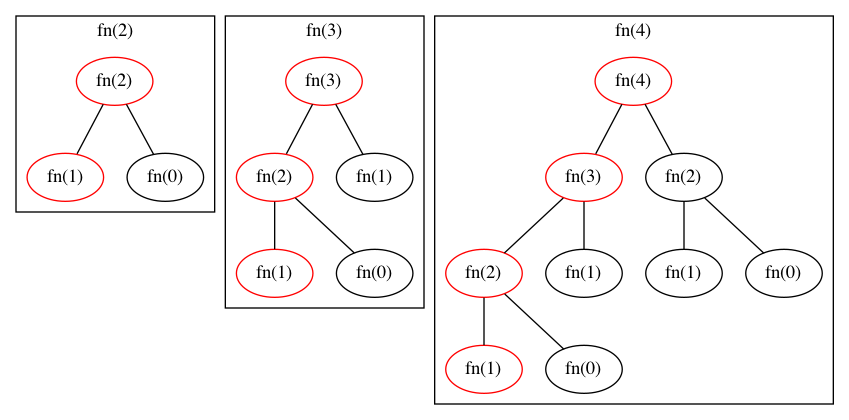
If you take a look at the generated tree calls, the leftmost nodes get down in descending lodge: fn(4), fn(3), fn(2), fn(1), which ways that the height of the tree (or the number of levels) on the tree will be n.

The total number of calls, in a complete binary tree, is two^n - 1. As you can see in fn(iv), the tree is not complete. The last level volition merely take two nodes, fn(1) and fn(0), while a complete tree would have eight nodes. But still, we can say the runtime would be exponential O(ii^n). Information technology won't go any worst because 2^northward is the upper bound.

Summary

In this chapter, we learned how to calculate the time complication of our code when we have the following elements:

• Basic operations like assignments, fleck, and math operators.
• Loops and nested loops
• Office invocations and recursions.

If you want to see more code examples for O(due north log n), O(n^two), O(due north!), check out the most common time complexities that every developer should know.

sanchezfition72.blogspot.com

Source: https://adrianmejia.com/how-to-find-time-complexity-of-an-algorithm-code-big-o-notation/

Share this post